Chapitre 26

Les Opérations sur la Matière

et le Vide

Opérations Booléennes

 

1 - Opérations sur la Matière et le Vide

 

2 - Opérations Booléennes

 

Retour au sommaire principal

 

Les Booléennes, ou Booliènnes, sont des opérations relatives aux théories de Georges BOOLE, logicien et mathématicien britannique (1815-1864).

 

Soit C l'objet résultant d'une opération entre deux objets A et B. L'opérateur booléen de 3D Turbo comporte 10 opérations :

 

	l'union (ou fusion) de 2 solides A et B	C = A U B
	l'intersection de 2 solides A et B	C = A ∩ B
	la soustraction de 2 solides A et B	C = A - B C = B - A
	la soustraction ouverte de 2 solides A et B	C = A - B C = B - A
	la soustraction sur l'enveloppe, peau de A la soustraction sur l'enveloppe, peau de B	C = A - B C = B - A
	la section commune - Profil d'intersection (ET exclusif)	C = A et B
	la différence symétrique de 2 solides A et B (OU exclusif)	C = A xor B

Avec les opérations booléennes, 3D Turbo est non seulement un logiciel 3D "surfacique" mais également un logiciel 3D "volumique", ce qui signifie qu'il faut raisonner "Matière" et "Antimatière".

 

Les opérations booléennes de 3D Turbo fonctionnent sur les volumes (surfaces fermées) et les surfaces ouvertes.

 

La "Matière" n'existe que par rapport à "l'Antimatière", le "Plein" par rapport au "Vide",. "l'Intérieur" par rapport à "l'Extérieur". "Matière, Plein, Intérieur" sont des synonymes désignant la partie solide d'un objet. "Antimatière, Vide, Extérieur, Creux, Poche" sont des synonymes désignant l'espace dépourvu de matière.

 

 

L'enveloppe (ou peau) délimite l'intérieur de l'extérieur.

 

Cette partie n'a aucune épaisseur. Elle permet simplement de représenter la matière. Dans 3D Turbo, cette partie est appelée "Surface", d'où le qualificatif de "Surfacique" quand la notion de "Solide" n'existe pas.

 

 

 

Dans 3D Turbo, c'est l'orientation des "Normales" aux surfaces qui différencie le coté matière du côté antimatière :

 

Par "solide", nous désignons la matière de l'objet, pour faire ressortir la notion de "peau" qui n'est que le reste de l'enveloppe de l'un des deux objets.

 

 

Soit deux objets A et B, dont les normales sont orientées vers l'intérieur, donc des objets solides.

 

		Union de solides#
		1 - Union de solides - Addition Booléenne

L'union ou fusion de A et B, notée A U B (A union B), est formée des éléments de l'ensemble C qui appartiennent à A ou à B (à au moins l'un des deux).

 

 

		Intersection de solides#
		2 - Intersection de solides - Partie commune

L'intersection de A et B, notée A ∩ B (A inter B), est formée des éléments de l'ensemble C qui appartiennent à la fois à A et à B (ensemble des éléments communs).

 

 

		Soustraction de solides#
		3 - Soustraction de solides.

La différence (ou soustraction) entre A et B, notée A - B (A moins B), est formée des éléments de C qui sont eux-mêmes :

 

-  soit des éléments de A qui n'appartiennent pas à B

-  soit des éléments de B qui n'appartiennent pas à A

 

 

		Soustraction sur l'enveloppe#
		4 - Soustraction sur l'enveloppe - Peau de A-B

La différence (ou soustraction) entre A et B, notée A - B (A moins B), est formée des éléments de C qui sont eux-mêmes :

 

-  soit des éléments de l'enveloppe (ou peau) A qui n'appartiennent pas à B

-  soit des éléments de l'enveloppe (ou peau) A qui appartiennent à la fois à A et à B

 

 

		Soustraction Inverse sur l'enveloppe#
		5 - Soustraction Inverse sur l'enveloppe

-  soit des éléments de l'enveloppe (ou peau) B qui appartiennent à la fois à A et à B

-  soit des éléments de l'enveloppe (ou peau) B qui n'appartiennent pas à A

 

 

		Profil d'intersection#
		6 - Section commune (ET exclusif) - Profil d'intersection

La section commune entre A et B, notée A et B, est formée des éléments de l'ensemble C qui appartiennent à la fois aux deux objets A et B.

 

 

		Différence symétrique de solides#
		7 - Différence symétrique de solides (OU exclusif)

La différence symétrique de A et B, notée A xor B, est formée des éléments de l'ensemble C qui appartiennent à l'un des deux objets A ou B et à un seul.

 

La notion de "Matière" et "d'Antimatière" a une importance primordiale dans le résultat des opérations booléennes.

 

Voici un exemple de fusion sur deux objets A et B.

 

La combinaison des cas d'orientations de leurs normales offre quatre résultats différents:

 

 

 

 

 

 

 

 

 

Une sphère dont les normales sont orientées vers l'extérieur, représente en réalité un cube infini, avec une poche sphérique (vide) en son milieu.

 

N'ayant pas d'autre moyen pour représenter cet infini, nous dessinons ce qui a une échelle humaine "la poche".

 

C'est en fonction de cette contrainte que les objets créés dans 3D Turbo par une opération booléenne sont différents.

 

Si les normales des deux objets A et B sont orientées vers l'intérieur, c'est à dire que l'enveloppe dessinée représente l'extérieur des objets, la fusion qui en résulte s'appréhende aisément.

 

Par contre, dans les trois autres cas, il faut penser constamment qu'on ne peut représenter que le "Vide" qui en résulte, d'ailleurs c'est aussi la représentation de l'extérieur des objets.

Les éléments géométriques mis en œuvre dans les opérations booléennes doivent répondre à des critères topologiques rigoureux, faute de quoi l'opérateur de calcul risque de produire des erreurs ou des résultats inattendus.

 

Les critères suivants doivent impérativement être respectés. Toute erreur produite par une opération booléenne doit conduire l'opérateur à vérifier immédiatement la validité des objets impliqués dans l'opération.

Les objets utilisés dans une opération booléenne doivent remplir les conditions suivantes :

 

-  Les éléments A et B doivent être des OBJETS répertoriés (voir le chapitre "Les Objets").

 

-  L'orientation des normales des objets doit être homogène et refléter le sens souhaité pour la matière. Le logiciel tentera de corriger automatiquement le sens des normales d'un objet non homogène. Cependant, cette correction peut être incomplète, impossible ou conduire à un sens matière opposé à celui souhaité en réalité. C'est pourquoi il est préférable de contrôler soi-même l'orientation des normales

 

 

-  Les objets peuvent être "FERMÉS" ou "OUVERTS"

 

Un objet ouvert est un objet dont la peau présente un trou.

 

Ca peut être un objet fermé à l'origine, dont on a enlevé une ou des facettes.

 

Ca peut être également un objet ayant deux arêtes superposées, (objet de révolution comme une sphère, avec profils 0 et 360 superposés) :

 

-  L'objet peut être réduit à un Plan (le plus simple des objets ouverts)

 

-  Les objets peuvent être constitués de plusieurs parties physiquement disjointes, regroupées sous un même nom d'objet

 

Remarque : Certains objets constitués de plusieurs solides, peuvent être parfois considérés soit comme "OUVERTS" soit comme "FERMÉS", le résultat n'étant pas du tout le même.

 

Soit un objet (A) constitué de deux cubes, ayant une facette adjacente, dont les points sont doublés :

 

 

Si on supprime l'une des deux facettes centrales, l'objet (A) peut être soit "OUVERT" soit "FERMÉ".

Voici le résultat d'une fusion entre les objets (A et B) si (A) est déclaré fermé.

 

Le logiciel en apprenant la forme de l'objet (A) a ignoré la partie de gauche, considérant qu'elle n'était pas cohérente avec le reste.

 

 

Voici le résultat d'une fusion entre les objets (A et B) si (A) est déclaré ouvert.

 

L'orientation de la facette centrale n'a pas d'importance, car le logiciel la corrige de lui-même.

 

 

-  Les objets ne doivent pas s'auto-intersecter.

 

 

-  Les objets ne doivent pas contenir de facettes en éventail sur une arête commune (cloisons).

 

 

-  Les objets ne doivent pas contenir des facettes adjacentes par un point.

 

 

 

-  Les objets ne doivent pas contenir des facettes fortement gauches.

 

-  Si un objet est ouvert, la ligne de coupe ne doit pas passer par l'ouverture.

 

 

 

-  Les objets peuvent résider dans des calques différents

		Orientation Automatique des Normales#
		1 - Orientation Automatique des Normales

Après qu'un objet a été créé par la voie géométrique ou surfacique, il est parfois nécessaire d'homogénéiser l'orientation des normales de ses facettes en vue de son utilisation par les opérations booléennes, ou pour un rendu photoréaliste.

 

· Sélectionner l'objet à orienter.

 

· Cliquer dans l'icône .

 

Vérifier que les normales aient bien été orientées dans le sens matière désiré, sinon inverser toutes les normales de l'objet.

		Vérifier un objet#
		2 - Vérifier un objet

Après qu'un objet a été créé par la voie géométrique ou surfacique, ou après qu'une opération booléenne a donné un résultat inattendu ou une erreur, il est nécessaire de vérifier s'il répond aux critères topologiques requis pour son utilisation en vue de son utilisation par les opérations booléennes.

 

· Sélectionner l'objet à orienter.

 

· Cliquer dans l'icône .

 

Observer la création de nouveaux objets de type CNX. Ils représentent :

 

-  soit les parties physiquement séparées de l'objet

-  soit les parties d'objets constituant des anomalies topologiques (cloisons)

 

Vérifier si les objets CNX sont normaux et acceptables (objets multi-composants) ou bien s'il s'agit de parties indésirables (cloisons,..)

 

Si des parties CNX sont jugées indésirables :

 

· Utiliser la fonction de nettoyage d'objet

		Nettoyer un objet#
		3 - Nettoyer un objet

Si un objet contient des éléments détectés comme topologiquement inacceptables (cloisons CNX, etc), cette fonction va séparer ces éléments de l'objet et les mettre dans un autre objet de type CNX.

 

· Sélectionner l'objet à orienter.

 

· Cliquer dans l'icône .

 

A l'issue de cette opération, l'objet initial aura donc été nettoyé de ses éléments indésirables et sera considéré comme bon pour les opérations booléennes.

		Réaliser une Opération Booléenne#
		1 - Réaliser une Opération Booléenne

Pour réaliser une opération booléenne, préparer 2 objets répondant strictement aux critères et restrictions énoncés plus haut.

 

· Cliquer sur l'une des icônes

 

En suivant les indications affichées dans la barre d'états :

 

· Pointer un nœud du premier objet (valider par Entrée si l'option Valider choix objets a été cochée).

 

· Pointer un nœud du second objet (valider par Entrée si l'option Valider choix objets a été cochée).

 

Remarque : Si un objet est hiérarchique, la sélection d'objets dans une opération booléenne sélectionne d’abord l'objet père au point cliqué tout en préservant la possibilité de cliquer successivement pour atteindre les fils si l'option validation du choix des objets est active.. (Option+Clic dans ) Voir le paragraphe Réglage des fonctions interactives du chapitre 8 - Créer des Entités.

 

Le dialogue suivant est proposé :

                                

 

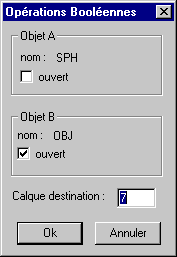
· Vérifier que les noms d'objets affichés sont bien ceux des objets à booléer.

 

Les cases à cocher ouvert sont renseignées pour information, selon que les objets désignés ont été détectés comme étant ouverts ou non.

 

· Indiquer le numéro du calque dans lequel l'objet résultant sera créé (le prochain calque libre est proposé d'office).

 

Les objets générateurs ne sont jamais effacés ni modifiés.

 

· Cliquer OK pour déclencher le calcul de l'opération.

 

Les calculs sont animés à l'écran.

 

On peut observer les différentes phases de l'opération :

 

-  Analyse topologique des volumes de chaque objet

-  Nettoyage de la zone d'intersection

-  Détermination du profil d'intersection

-  Génération de l'objet résultant dans le calque destination

 

Sélectionner le calque destination en mode Courant et observer le résultat.

 

Si ce résultat ne correspond pas à ce qui est attendu :

 

· Vérifier la constitution des objets à l'aide des outils de vérification.

 

· Chasser les facettes nulles (facettes sans surface).

 

· Chasser les facettes gauches.

 

· Trianguler les objets.

ou

· Appliquer un infime déplacement à l'un des deux objets.

 

· Recommencer l'opération.

 

L'une des dispositions ci-dessus suffit très souvent à régler une situation d'erreur.

		Charte des Opérations Booléennes#
		2 - Charte des Opérations Booléennes

Le tableau ci dessous indique le résultat des opérateurs booléens en fonction du sens matière des objets.

 

Opération	A U B	A ∩ B	A - B	B - A	A - B ouvert	B - A ouvert	A - B peau	B - A peau

 

Les opérations de calcul de profil et de OU exclusif génèrent toujours le même résultat et ne sont donc pas représentées dans ce tableau.

		Exemples d'Opérations Booléennes#
		3 - Exemples d'Opérations Booléennes

Voici plusieurs exemples du rôle fondamental de l'orientation des facettes dans le résultat d'une opération de FUSION :

 

 

 

 

 

 

 

 

 

 

 

 

 

La section contient des points qui appartiennent à la fois à l'objet A et à l'objet B.

 

Elle peut servir comme parcours pour un tubage.

 

L'opérateur produit toujours 2 profils strictement superposés, un pour chaque objet.

 

Il est nécessaire de fusionner ces profils à l'aide de la fonction d'optimisation du modèle appliquée au calque contenant les profils.